지구를 만들어보자.
아무것도 없는 공간에 구를 그리고 지구의 이미지를 덮어씌워보자. 낮과 밤을 촬영한 NASA 이미지 두 장을 태양이 비추는 곳과 그렇지 않은 곳에 적절히 맵핑해주자. 그리고 두 부분이 만나는 곳을 황혼처럼 약간 붉게 만들어보자. 푸르스름한 지구 주변의 대기도 표현하면 그럭저럭 완성이 된다.
아, 당연히 연월일시에 따라 지구의 상태가 변해야 한다.
cpp에서 OpenGL 라이브러리를 사용하여 만들었다. OpenGL에서 직접적으로 코딩하는 사람들에게는 도움이 되겠지만, 그런 사람은 많지 않을테니... WebGL 사용자들은 비슷하게 응용할 수 있을 것 같고, 안써봐서 잘 모르겠지만 유니티나 언리얼엔진같이 셰이더 기반으로 작업하는 환경에서도 적절히 옮겨쓸 수 있을 것 같다.
1년 전쯤 한 포럼에서 설명하면서 짧게 언급한 부분에 살을 약간 더 입혀봤다. 글의 중간에 뜬금없이 파워포인트 화면 같은 것들이 등장하는데 발표자료가 기본이라 그렇다.
어차피 코드는 그다지 복잡한게 없으므로, 지구를 '지구스럽게' 표현하기 위해서 고려해야 할 요소 몇 가지를 설명하는 글이 될 것 같다. 온전한 코드를 올려놓지는 않았지만, 시간이 한참 걸렸던 핵심적인 부분들은 모두 들어있다.
태양빛이 바다에 반사될 때 나타나는 specular 표현만 안 썼는데, 이런 부분은 구 표현에서 라이팅과 렌더링의 기본이므로 조금만 찾아보면 여기저기에서 설명한 글이 많이 나온다.
전체적인 순서는 아래와 같다. 크게 세 단계와 마지막의 미세한 조정으로 이루어진다.
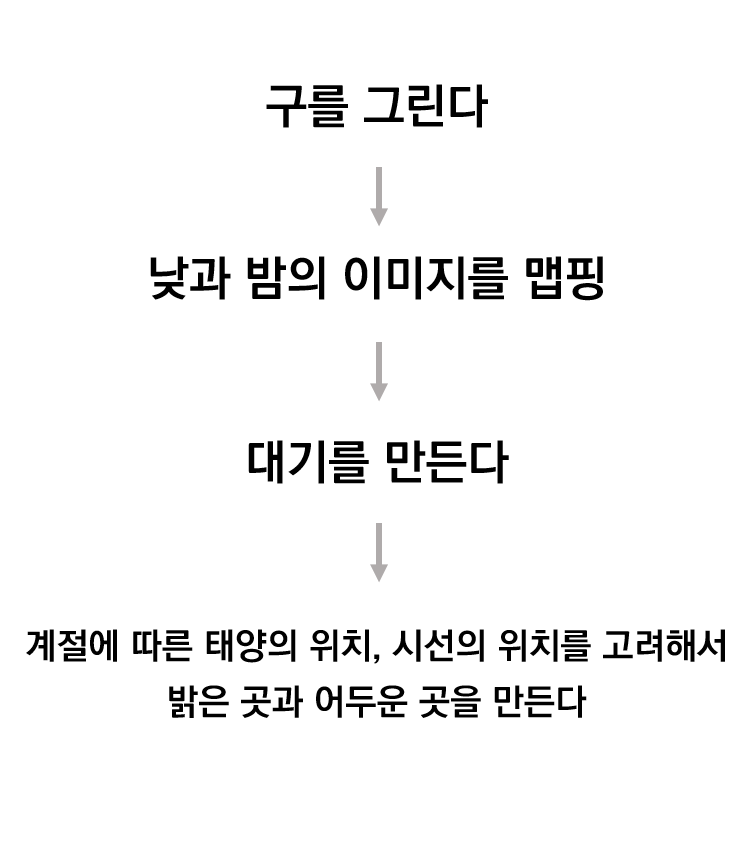
마지막 단계라고 설명한 부분은, 사실 두번째 세번째 단계에 이미 포함되어 있다. 낮과 밤의 이미지를 맵핑할 때 태양의 위치에 따라서 두 이미지의 픽셀값을 취사선택해야 하기 때문에 이미 수식에 해당 변수들이 포함되어 있어야 한다.
구를 그린다
사실 구를 그리는건 웬만한 프로그램들에서 클릭 한두번으로 가능하다. 다만 맨바탕에 그리려다보면, 삼각형만으로 구를 만들어내야 한다. 이미 알려진 알고리즘이 많지만, 어떻게 그리는게 여러가지 대응에 효율적일지 고민을 하게 된다. 다행히 이런 기본적인 내용들은 대부분 세상의 똑똑하면서 친절하기까지 한 사람들이 이미 자세히 설명을 해놓았다. 찾기만 잘 찾으면 된다.
여기서는 아래의 글에 설명된 방식을 따랐다.
Drawing Sphere in OpenGL without using gluSphere()?
Are there any tutorials out there that explain how I can draw a sphere in OpenGL without having to use gluSphere()? Many of the 3D tutorials for OpenGL are just on cubes. I have searched but most ...
stackoverflow.com
이미지 몇장과 대략적인 설명을 옮겨보겠다.

구를 그리든, 휘어진 화살표를 그리든, 셰이더에서 기본적인 표현은 크기가 1인 단위공간 안에서의 벡터로 표현될 때가 많다. 여기서도 반지름이 1.00 인 구를 그린다. 단위 크기의 구만 그린 후, 나중에 지구 반지름을 곱해주기만 하면 된다.
기본적인 기하학적인 알고리즘들은 보고 있자면, '오 그렇지 그렇지, 그렇게 하면 이렇게 되겠네. 와 신기한데.'라고 감탄하게되는 경우가 많은데 이 알고리즘 역시 그렇다.
정팔면체를 이루는 삼각형 하나씩마다 변의 중점을 분할한 후, 원점으로부터 그 중점까지의 거리를 1로 만들고, 그렇게 네 개로 분할된 삼각형 하나하나를 같은 방식으로 분할해가다보면 구가 만들어진다. 몇 번을 분할하느냐에 따라 구의 디테일이 결정된다.
주요한 함 수 두개는 아래와 같다. 첫 호출 함수와 재귀적으로 호출되는 subdivide 함수 두개로 이루어진다.

첫단계에서는 정팔면체를 이루는 8개 삼각형 각각의 정점 위치를 입력한 subdivide함수 8개를 하나씩 호출해준다. 3차원 공간상의 기준점을 (0,0,0)으로 두고 삼각형 각각의 정점 좌표 3개의 x,y,z좌표를 나란히 입력했다.
루프와 배열로 해도 될 것 같은데, 저렇게 두는게 나중에 가독성 측면에서 조금 더 나을 것 같았다. 실행속도가 떨어지는 것도 아니니.
여기서는 7단계로 호출했으며, 마지막 단계로 내려가면 가장 작은 최종 삼각형들을 vertex_position 배열에 저장한다. 3년 전쯤에 만들었던 함수인데, 다시 보니 vertex_index는 사실 counting 용도뿐이라 굳이 저렇게 안 더해도 될것 같다. (index drawing으로 하려고 했던 것 같은데, 결국 정점이 모두 들어가서 vertex reuse가 되지 않는 상황이다)
재귀적 호출을 통해 마지막 레벨인 if (level==0) 구간에 도달하게 되면, 각 정점의 좌표를 normalize 하는 과정을 거쳐 배열에 입력된다. 이 정점은 glDrawArrays를 통해 그대로 셰이더로 보내고, 지구의 반지름은 셰이더에서 곱해주게 된다.
태양의 위치를 구해보자
이미지를 매핑하기전에 먼저 셰이더 밖에서 태양의 위치를 구해보자.
//태양 위치를 구한다.(빛의 방향을 구한다.)
time_t realTime = timeSimul + timeZero;
struct tm *d = localtime(&realTime);
int nTHday = d->tm_yday;
glm::mat4 sunDeclination = glm::rotate(glm::mat4(1.0f),
glm::radians((float)(23.44f * cos(2.0f*M_PI/365.0f * (nTHday+10.0f)))),
vec3(0.0f, 1.0f, 0.0f));
glm::mat4 lightRotation = glm::rotate(glm::mat4(1.0f),
glm::radians((timeSimul+43200) / 86400.0f * -360.0f),
vec3(0.0f, 0.0f, 1.0f));
vec4 lightDirection = lightRotation * sunDeclination * vec4(1.0, 0.0, 0.0, 1.0);수식이 복잡해보이지만 천동설(!) 개념의 세상, 즉 지구의 중심이 (0,0,0) 인 세상에서 태양을 지구 주변으로 돌리는 공식이다. 지구는 23.44도 기울어졌고... 처음에 좌표값을 어디를 0,0으로 설정했는지에 따라 반바퀴 돌려주고.... 그런 수식들이 들어간다. 특별히 계산법이 아니라 매우 일반적인 태양 위치 계산법이다. (다시 보니 윤년과 관계된 처리를 2018년 근처에 맞게 적당히 처리했다.(nTHday * 10.0f 부분) 시간이 있을 때 다시 고쳐봐야겠다)
방향벡터를 계산하는 것이므로 지구와 태양의 거리는 신경쓰지 않아도 된다.
light direction 값은 각각의 셰이더에 uniform 변수로 넣어준다.
세계지도를 선으로 표현해보자
세계지도 shape 파일은 아래의 사이트에서 구할 수 있다.
Natural Earth - Free vector and raster map data at 1:10m, 1:50m, and 1:110m scales
Natural Earth is a public domain map dataset available at 1:10m, 1:50m, and 1:110 million scales. Featuring tightly integrated vector and raster data, with Natural Earth you can make a variety of visually pleasing, well-crafted maps with cartography or GIS
www.naturalearthdata.com
WGS84 형식으로 읽은 후, 셰이더에서 아래와 같은 변환을 통해 그렸다.
지구 중심을 원점(0,0,0)으로 두는 계산법이다.
#define M_PI 3.14159265358979323846
#define WGS84_EQUATORIAL_RADIUS 6378137.0
layout(location = 0) in vec3 pos;
vec3 geodeticToCartesian(float longitude, float latitude, float metersElevation) {
float cosLat = cos(latitude * (M_PI / 180));
float sinLat = sin(latitude * (M_PI / 180));
float cosLon = cos(longitude * (M_PI / 180));
float sinLon = sin(longitude * (M_PI / 180));
//모두 장반경으로 계산한 약식임
float x = (WGS84_EQUATORIAL_RADIUS + metersElevation) * cosLat * cosLon;
float y = (WGS84_EQUATORIAL_RADIUS + metersElevation) * cosLat * sinLon;
float z = (WGS84_EQUATORIAL_RADIUS + metersElevation) * sinLat;
return vec3(x,y,z);
}
낮과 밤의 이미지를 맵핑해보자
이제 지구의 이미지를 씌워보자.
아래의 NASA 사이트를 여기저기 돌아다니다보면 목적에 맞는 여러가지 적절한 이미지들을 찾아볼 수 있다.
NASA Visible Earth - Home
visibleearth.nasa.gov
여기서는 아래의 두 가지 이미지를 선택했다.

이 이미지들은 간단한 변환으로 경위도 좌표를 0~1 사이의 매핑좌표에 대응시킬 수 있도록 만들어진 이미지들이다.
앞에서 만든 정점들을 vertex shader에서 곧바로 fragment shader로 보낸다. 이 좌표들을 경위도 좌표로 변환시켰다.
fragment shader의 일부를 옮겨보면 아래와 같다.
layout (binding = 0) uniform sampler2D dayTexture;
layout (binding = 1) uniform sampler2D nightTexture;
in Vertex
{
vec4 position;
} vertex;
void main() {
vec2 longitudeLatitude = vec2((atan(vertex.position.y, vertex.position.x) / 3.1415926 + 1.0) * 0.5,
(asin(vertex.position.z) / 3.1415926 + 0.5));
vec3 dayPic = texture(dayTexture, longitudeLatitude).rgb;
vec3 nightPic = texture(nightTexture, longitudeLatitude).rgb;
vec3 normal = normalize(vertex.position.xyz);
vec4 theColor = vec4(ColorDayNight(dayPic, nightPic, normal),1.0);
}아크탄젠트와 아크사인 함수를 통해서 x,y,z 좌표를 경도와 위도로 변환시키면 래디안 값으로 떨어지므로 다시 pi(3.141592)로 나눈 후 더하고 곱해서 매핑 좌표 범위인 0~1 사이로 변환시킨다. 그 결과가 longituteLatitude 변수에 담겼다.
dayTexture에는 낮의 이미지가, nightTexture에는 밤의 이미지가 담겼다. 현재 프래그먼트에 해당하는 픽셀값들을 추출한 후 ColorDayNight 함수에 보낸다. 이 함수에서 태양의 위치등을 고려해서 최종적으로 낮을 쓸지 밤을 쓸지 둘을 적절히 섞은 후 다른 색을 덧바를지 결정하게 된다.
함수는 아래와 같이 결정했다.
vec3 ColorDayNight(vec3 objectC1, vec3 objectC2, vec3 normal)
{
return 1.0 *(
objectC1 *(max(0.0,dot(lightDirection, normal)))
+ objectC2 * (max(0.0,dot(-lightDirection, normal)))
//+vec3(1,0.25,0.1) *max(0.0, pow( 0.80* (1.0- abs(dot(lightDirection,normal))) ,12.0))
);
}
빛의 위치는 밖에서 계산한 후 셰이더에 uniform 변수로 집어넣는다.
빛의 방향은 낮과 밤을 각각 반대로 적용시켜주고, 함수에 매개변수로 집어넣은 정점 값과 빛의 방향을 내적해서 최종적으로 낮과 밤 이미지에 각각 얼마만크의 가중치를 주게될지 결정했다.
max 함수를 사용해서 음수 값이 나오지 않도록 했다.
그러면 아래와 같은 지구가 그려진다. 우측은 태양빛을 받는 낮, 좌측은 밤이다.

여기까지가 기본인데, 여기에 한 가지 표현을 더했다.
황혼(twilight zone)인데, 해줘도 되고 안해줘도 큰 상관은 없겠다. 실제로 우주에서 저렇게 보이는 것 같지는 않지만, 낮과 밤의 경계를 그냥 두기 밋밋해서 넣어봤다. 위의 코드에서 주석 부분을 풀면 아래와 같은 이미지로 맵핑된다.

다 된 것 같지만 어딘가 많이 밋밋하다. 대기가 없는 지구처럼 보이지 않는가.
이제 마지막으로 대기를 표현해보자
시선 방향에서 보이는 반구를 그린 후, 반구에 가장자리 부분에 중점을 두어 맵핑하기로 한다. 렌더링에서 흔히 rim이라고 부르는 표현이다.
반구는 앞에서 정팔면체로 출발하지 말고 삼각형 네개에서 출발시켜 만들어도 되고, 앞서 만들었던 구에서 노말벡터가 시선쪽으로 향한 것들만 취해서 사용해도 된다.
반구의 크기는 지구 반지름 6378km 보다 150km 큰 6528km로 두고 그렸다. 대기권의 높이를 보통 100km로 보는데, 그렇게 두었더니 약간 밋밋해서 50km 더 설정했다. 좀 더 정확한 표현이 필요할 때는 실제 우주에서 관찰되는 대기가 어느 높이까지인지 알아본 후 결정해야 할 것 같다.
색상은 vertex shader에서 결정한다.
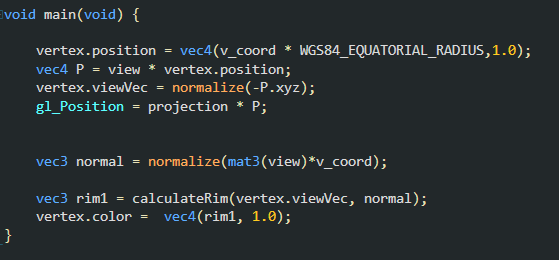
아래와 같이 뷰벡터와 정점 노말벡터를 계산해서 rim 값을 계산하는 함수로 보낸다.
view 변수는 modelview 매트릭스다.

과학적인 사실이 중요한 시각화라면 좀 더 대기에 대해서 공부해야 할 것 같다. 여기서는 우주에서 본 지구 이미지들을 조금 찾아보고 약간의 시행착오를 거쳐 비슷하게 나오도록 했다. 주석으로 처리된 부분은 시행착오 과정이다.
기본 색상값을 구한 후에는 역시 fragment shader로 보내서 태양위치와의 상호작용을 계산한다. 낮 부분의 대기는 좀 더 밝게, 밤 부분의 대기는 좀 더 어둡게 만들어주었다.

위의 이미지가 낮과 밤 이미지 없이 가장자리 부분만 표현한 이미지다. (선으로 된 지도가 지구 반대편과 겹쳐서 약간 복잡하게 보인다.)
이제 낮과 밤 이미지도 다시 활성화시켜보자.
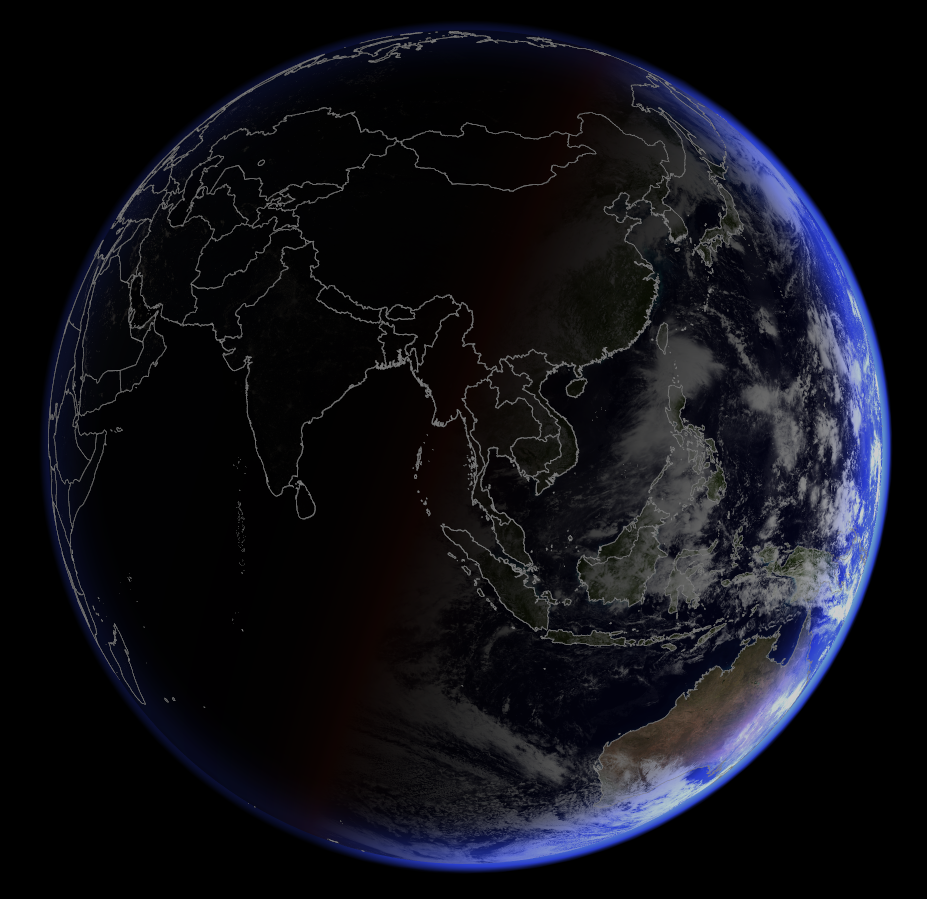
대기 부분을 확대해보자.

그럭저럭! 지구가 완성되었다.
여러가지 지구와 그 위의 데이터
이제 색상값들을 조정해보면서 자신만의 지구, 혹은 겹쳐지는 데이터들과 어울리는 색상의 지구를 만들 수 있다.

지구가 만들어지면 그 위에 여러가지 데이터를 올려볼 수 있다.
항공노선도 테스트 시각화

코로나 전후 항공기 이동량 비교

영상은 아래.
2019년 UN migrant stock data
https://www.un.org/en/development/desa/population/migration/data/estimates2/estimates19.asp
처음 보이는 이미지는 문턱값을 50만명에서 자른 것.
화살표 그리는데 좀 힘들었다. 그런데 하다가 마무리를 못한 시각화

'Function' 카테고리의 다른 글
| 겹치지 않는 원으로 인구 그려보기 (0) | 2021.12.29 |
|---|---|
| 반응형 유동인구/매출액 Viewer (0) | 2021.12.20 |
| 스마트서울 도시데이터센서(S-DoT)기온 데이터 시각화 (6) | 2021.10.11 |
| OD 시각화 3 : 서울 생활이동 데이터를 지도 위에 옮겨보자 (4) | 2021.09.10 |
| 15분만에 전국 음식점 개폐업 지도 만들어보기 (4) | 2021.07.12 |




