여기서는 시군구 인구를 원으로 시각화한 과정의 기술적인 내용에 대해 적어보겠다.
관련된 두 글은 다음과 같다.
대한민국 시군구 인구 변화 시각화(1975~2020)
우리나라 인구 변화를 지도 위에 시군구 단위로 시각화 한 이 글에 새로운 발견은 없다. 인구 변화에 관심있던 사람이라면 대부분 아는 내용이다. 서울-인천-경기를 포괄하는 '수도권'으로 인구
www.vw-lab.com
시군구별 연령별 인구 변화 시각화(2000~2020)
앞의 글에 이어 이번에는 성연령별로 구분해본 인구의 변화를 본다. 앞의 글(아래 링크)에서 대체적인 취지와 개요를 설명했다. 대한민국 시군구 인구 변화 시각화(1975~2020) 우리나라 인구 변화
www.vw-lab.com
데이터
두 글에서 사용한 데이터가 다르다.
첫번째 1975년~2020년의 시군구 인구는 다음의 데이터 두 개를 결합했다.
1. 2010년 행정구역 기준 1975~2010년 시군구 인구
KOSIS
kosis.kr
2. 2015~2020년 시군구 인구
KOSIS
kosis.kr
행정구역은 2020년 기준으로 재조정해서 사용했다.
1번 데이터는 이미 2010년 기준으로 재조정되어 있으며 2번 데이터부터는 직접 조정했다. 예를 들어 세종시는 2012년에 신설되었으므로 2011년까지는 연기군의 데이터를 사용했다. 물론 세부적인 경계가 다르지만 이 부분은 그냥 무시하고 진행했다. 과거의 청원군과 청주시를 청주시 전체로 맞추는 등 약간의 수동적인 조정을 했다.
수원, 성남, 고양, 전주, 포항 등 250개 시군구 기준으로는 하위의 행정구들이 존재하는 지역들은 하나로 합쳐주었다. 원래 이렇게 하면 228개 기초자치단체가 되는데, 제주도의 경우 행정시인 제주시와 서귀포시를 별도로 구분해서 229개 시군구로 작업했다. 특별한 이유가 있는 것은 아니고... 하다보니 그렇게 되었다.
데이터는 아래 링크에 있다.
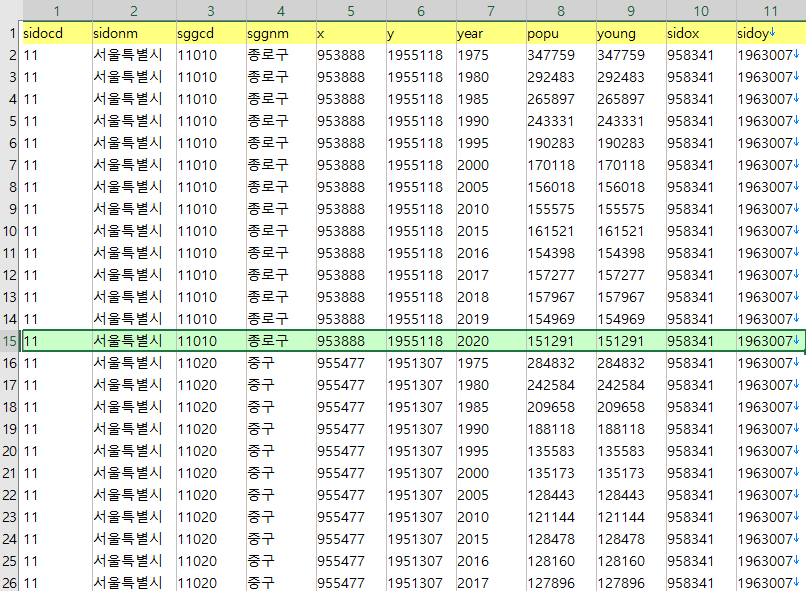
원을 그릴 시군구 중심점과 시도 중심점을 지도에서 별도로 추출하여 함께 넣어주었다. 좌표계는 UTMK(EPSG:5179)다.
(young이라고 된 컬럼은 지금은 쓸데없는 dummy 같은 부분이다. 같은 시각화 코드에서 자료를 읽다보니 형식을 맞춰주는게 편해서 그렇게 했다.)
두 번째 2000~2020년 성연령별 데이터는 SGIS에서 신청해서 받았다.
자료제공|통계지리정보서비스
통계지리정보시스템에서는 더이상 지도 데이터를 제공하지 않습니다. 지도 데이터가 필요하신 사용자께서는 링크된 설명서를 다운로드 받아 도로명 지도를 신청하시기 바랍니다.
sgis.kostat.go.kr
위의 링크에서 2021년 기준 2000~2020년의 집계구별 인구 데이터를 받을 수 있다.
집계구별 인구이므로 집계구코드의 첫 다섯자리를 끊어서 시군구로 재집계하면 된다. 문제는 N/A로 표시된 5인 미만 인구인데, 그냥 2.5명으로 일괄적으로 처리했다. 통계청 국가통계포털에서 실제 시군구별 인구와 비교해보면 약간의 차이가 있다. 굳이 집계구별 인구 데이터를 사용한 이유는 현재 행정구역 기준으로 재집계 되어 있기 때문이다. 그렇게 된 자료가 있어야 시계열을 연계한 그림을 그릴 수 있다.
내려받은 자료 중 [2021년기준_2000년_성연령별인구.txt]와 같은 자료들을 다음의 코드들로 처리했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
|
rawFolder <- "X:\\#DB_SET\\통계청 인구\\2021년 기준 과거 인구\\"
workFolder <- "A:/work/"
if (exists("finaldata")) rm(finaldata)
years <- c(2000,2005,2010,2015,2016,2017,2018,2019,2020)
for (y in years) {
# 통계청 집계구별 인구를 읽는다.
fileName <- paste0(rawFolder,"2021년기준_",y,"년_성연령별인구.txt")
system.time(raw <- fread(fileName,
sep = "^", header = FALSE, stringsAsFactors = FALSE,
col.names = c('year','admcd','agecd','popu'),
colClasses = c('integer', 'character','character','character')))
#집계구별 총 인구를 계산한다.
#집계구별 인구 중 1~4인은 NA로 처리되어 있으므로 NA대신 2.5를 입력한다.
popu <- raw %>% mutate(code = as.integer(substr(agecd,8, length(agecd)))) %>%
filter(code<=21) %>% #21까지가 남녀인구 999는 자료없는 집계구
mutate(code = (code -1) * 5) %>%
mutate(sggcd = substr(admcd,1,5)) %>%
mutate(popu = replace_na(as.numeric(popu), 2.5)) %>%
group_by(sggcd, code) %>%
summarise(.groups="keep", popu = sum(popu)) %>%
ungroup()
popu <- popu %>% mutate(year = y)
if (exists("finaldata")) {
finaldata <- finaldata %>% bind_rows(popu)
} else {
finaldata <- popu
}
print(fileName)
}
#시도 중심점을 읽는다.
system.time(sidoxy <- fread(paste0(workFolder,"sidoxy.tsv"),
colClasses = list(character = c(1,2),
integer=c(3,4)),
sep = "\t", header = TRUE, stringsAsFactors = FALSE#, nThread = 30
))
##준비한 250 -> 229 시군구 매칭 데이터를 읽는다.
sggcdTbl <- fread(paste0(workFolder,"2021_sggcd_02.tsv" ),
sep = "\t", header = TRUE, stringsAsFactors = FALSE,
colClasses = c('character','character','character','character','character',
'integer','integer'))
temp <- finaldata %>%
group_by(year ) %>%
summarise(.groups="keep", popu = sum(popu))
temp <- finaldata %>% left_join(sggcdTbl, by = c("sggcd"="sggcd0")) %>%
ungroup()
temp <- temp %>% left_join(sidoxy %>% select(sido,sidox,sidoy), by =c("sidocd"="sido"))
#실제로 이용하지 않을 연도의 데이터를 만드는 함수. 1975~2020년 데이터와 같은 시각화 코드에 사용하기 위해 추가했다.
addDummy <-function(popuTable) {
years <- c(1975, 1980, 1985, 1990, 1995)
popudummy <- popuTable %>%
filter(year==2000)
for (yyyy in years) {
#yyyy<-1975
popudummy <- popudummy %>% mutate(year = yyyy)
popuTable <- popuTable %>% bind_rows(popudummy)
}
popuTable <- popuTable %>% arrange(sggcd, year)
return (popuTable)
}
popu0009 <- temp %>% filter(code<10) %>%
group_by(year, sggcd.y, sidocd,sidonm, sggnm, x, y, sidox, sidoy) %>%
summarise(.groups="keep", popu = sum(popu)) %>%
mutate(young = popu) %>%
select(sidocd,sidonm, sggcd=sggcd.y, sggnm, x, y, year,young, popu, sidox, sidoy ) %>%
ungroup()
popu0009 <- addDummy(popu0009)
popu0019 <- temp %>% filter(code<=15) %>%
group_by(year, sggcd.y, sidocd,sidonm, sggnm, x, y, sidox, sidoy) %>%
summarise(.groups="keep", popu = sum(popu)) %>%
mutate(young = popu) %>%
select(sidocd,sidonm, sggcd=sggcd.y, sggnm, x, y, year,young, popu, sidox, sidoy ) %>%
ungroup()
popu0019 <- addDummy(popu0019)
fwrite(popu0009, file=paste0(workFolder,"popu0009.tsv"),
quote=FALSE, sep = "\t", row.names = FALSE, col.names = TRUE)
fwrite(popu0019, file=paste0(workFolder,"popu0019.tsv"),
quote=FALSE, sep = "\t", row.names = FALSE, col.names = TRUE)
#각 연도의 상대적 비율 구하기 위한 함수
popuToRatio <- function(popuTable) {
popuSum <- popuTable %>%
group_by(year) %>%
summarise(.groups="keep", popuSum= sum(popu))
#곱해주는 숫자 10000000은 기존 시각화 코드와 원의 크기를 맞춰주기 위한 부분으로 큰 의미는 없다.
popuTable <- popuTable %>% left_join(popuSum, by = "year") %>%
mutate(popu = popu/popuSum * 10000000) %>%
mutate(young = popu)
return(popuTable)
}
popu0009R <- popuToRatio(popu0009)
popu0019R <- popuToRatio(popu0019)
fwrite(popu0009R, file=paste0(workFolder,"popu0009R.tsv"),
quote=FALSE, sep = "\t", row.names = FALSE, col.names = TRUE)
fwrite(popu0019R, file=paste0(workFolder,"popu0019R.tsv"),
quote=FALSE, sep = "\t", row.names = FALSE, col.names = TRUE)
|
cs |
통계청 데이터를 제외한 시군구 중심점과 위의 과정을 통해 만든 데이터들은 아래 링크에 있다.
2000~2020년의 마스다 지수를 계산하기 위한 데이터는 아래와 같이 가공했다. 원본은 위와 같은 SGIS 데이터다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
|
rawFolder <- "X:\\#DB_SET\\통계청 인구\\2021년 기준 과거 인구\\"
workFolder <- "A:/work/"
if (exists("finaldataF")) rm(finaldataF)
years <- c(2000,2005,2010,2015,2016,2017,2018,2019,2020)
for (y in years) {
# 통계청 집계구별 인구를 읽는다.
fileName <- paste0(rawFolder,"2021년기준_",y,"년_성연령별인구.txt")
system.time(raw <- fread(fileName,
sep = "^", header = FALSE, stringsAsFactors = FALSE,
col.names = c('year','admcd','agecd','popu'),
colClasses = c('integer', 'character','character','character')))
#집계구별 총 인구를 계산한다.
#집계구별 인구 중 1~4인은 NA로 처리되어 있으므로 NA대신 2.5를 입력한다.
popu <- raw %>% mutate(code = as.integer(substr(agecd,8, length(agecd)))) %>%
filter(code<=81 & code>=61) %>% #21까지가 남녀인구 999는 자료없는 집계구
mutate(code = (code -61) * 5) %>%
mutate(sggcd = substr(admcd,1,5)) %>%
mutate(popu = replace_na(as.numeric(popu), 2.5)) %>%
group_by(sggcd, code) %>%
summarise(.groups="keep", popu = sum(popu)) %>%
ungroup()
popu <- popu %>% mutate(year = y)
if (exists("finaldataF")) {
finaldataF <- finaldataF %>% bind_rows(popu)
} else {
finaldataF <- popu
}
print(fileName)
}
temp2 <- finaldataF %>% left_join(sggcdTbl, by = c("sggcd"="sggcd0")) %>%
ungroup()
popu6599 <- temp %>% filter(code>=65) %>%
group_by(year, sggcd.y, sidocd,sidonm, sggnm, x, y) %>%
summarise(.groups="keep", popu = sum(popu)) %>%
select(sidocd,sidonm, sggcd=sggcd.y, sggnm, x, y, year, popu ) %>%
ungroup()
popu6599 <- addDummy(popu6599)
popu2039F <- temp2 %>% filter(code>=20 & code<40) %>%
group_by(year, sggcd.y, sidocd,sidonm, sggnm, x, y) %>%
summarise(.groups="keep", popu = sum(popu)) %>%
select(sidocd,sidonm, sggcd=sggcd.y, sggnm, x, y, year, popu ) %>%
ungroup()
popu2039F <- addDummy(popu2039F)
popuMasda <- popu2039F %>% left_join(popu6599 %>% select(sggcd, year, popu), by = c("sggcd","year"))
colnames(popuMasda) <- c("sidocd","sidonm","sggcd","sggnm","x","y","year","young","popu")
popuMasda <- popuMasda %>%
mutate(popu = young + popu)
popuMasda <- popuMasda %>% left_join(sidoxy %>% select(sido,sidox,sidoy), by =c("sidocd"="sido"))
fwrite(popuMasda, file=paste0(workFolder,"popuMasda.tsv"),
quote=FALSE, sep = "\t", row.names = FALSE, col.names = TRUE)
|
cs |
앞의 코드에서 읽은 5세 연령별 인구와 시도중심점등이 있어야 사용 가능하다.

위와 같은 데이터에서 1975~1995년은 역시 같은 시각화 코드에서 읽기 위한 dummy 같은 부분이므로 신경쓰지 않아도 된다.
그렇게 만든 데이터는 아래 링크에 있다. 마스다 지수는 간단하지만, 아직 계산하지 않았다.
위의 데이터 기준으로는 young / (popu - young)을 하면 된다.
시군구를 원으로 그리기
각 시군구 인구를 겹치지 않는 원으로 그려보고자 한 출발점은, 아래와 같은 카토그램을 피해보고자 함이었다.

위 그림은 인구 수 비례로 시군구 면적을 재조정함으로써 기존 지리적 경계를 의도적으로 왜곡시킨 카토그램이다. 서울 인천 경기 등 수도권의 인구가 많다는 점은 충분히 강조가 되지만 바로 주변지역인 강원도나 충청도의 경우 형상과 지리적 위치를 알아보기가 어렵다. 특히 폭이 좁은 도형으로 길게 늘어질 경우 실제 면적을 직관적으로 알기가 어렵다.
그래서 아래와 같이 겹치지 않는 원으로 그렸다.

원의 크기를 적당히 조절함으로써 수도권 인구가 경기도 영역을 벗어나도록 할 수 있고, 벗어난 인구가 주변 지역을 밀고 들어가면서 인구의 과도함을 보여줄 수 있다. 수도권뿐만 아니라 다른 지역들도 인구의 변화를 어느정도 알아볼 수 있다. 광역시급 이상의 인구들이 많이 증가하고 다른 비도시 지역들의 인구가 줄어들었음을 볼 수 있다.
d3.js의 force layout 같은 라이브러리를 응용하면 그릴 수 있을 것 같기도 하다. 여기서는 cpp 기반의 OpenGL로 작업했다. 셰이더에서 작업하다보니 적절한 코드를 찾기 어려웠는데, 아주 간단한 알고리즘으로 될 것 같아서 그냥 곧바로 작성했다. 약간의 결함도 있지만 그럭저럭 돌아가서 그것으로 주욱 그렸다.
충돌과 좌표들을 계산하는 compute shader 코드는 다음과 같다.
어차피 229개 x 229개의 충돌만 계산하면 되기 때문에 성능은 신경쓰지 않고 작성했다.
처음에 적은 코드를 수정해가면서 계속 1회용처럼 작업하다보니 약간 지저분하게 되었다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
|
#version 460
#extension GL_NV_gpu_shader5 : require
#extension GL_NV_shader_atomic_float : require
layout(local_size_x = 256, local_size_y=1, local_size_z = 1) in;
struct SGGXY
{
float orix;
float oriy;
float floatx;
float floaty;
float altx;
float alty;
};
struct SGGPOPU
{
int index;
int sggcd;
int year;
int popu;
int popu2;
};
//base 좌표는 카텍 xy 100000,50000
layout(binding = 0) buffer xy0buffer {
SGGXY xy0[];
};
layout(binding = 1) buffer xy1buffer {
SGGXY xy1[];
};
layout(binding = 2) buffer popuBuffer {
SGGPOPU popu[];
};
layout(binding = 3) uniform atomic_uint atomicCnt;
layout(binding = 4) buffer sggIndexBuffer {
int sggidx[];
};
uniform int indexmax;
uniform ivec3 years;
uniform float radius;
uniform int center;
float popuToRadius(float popu)
{
return pow(float(popu), 0.5) * radius;
}
void main()
{
uint index = gl_GlobalInvocationID.x; //위와 같은 값임
if (index < indexmax) {
int index0 = (14 * int(index)) + years.x;
int index1 = (14 * int(index)) + years.y;
float popu0 = mix(popu[index0].popu, popu[index1].popu, years.z / 5.0f) ;
float popu1 = mix(popu[index0].popu2, popu[index1].popu2, years.z / 5.0f) ;
float popu1975 = popu[14*int(index)+0].popu; //1975년 기준
bool judge = popu1/(popu0-popu1) <0.5; //마스다 지수 0.5 미만
//bool judge = popu1975>popu0;
//judge= false;
//특정 값이 되면 체크
if (judge) {
sggidx[index] = 1;
}
float rd0 = popuToRadius(popu0);
vec2 xy00 = vec2(xy0[index].floatx, xy0[index].floaty);
int intersectCount = 0;
for (int i=0 ; i < 229 ; i++)
{
if (i==index) continue; //자기자신은 건너뛴다.
int indexT0 = (14 * i) + years.x;
int indexT1 = (14 * i) + years.y;
float popu1 = mix(popu[indexT0].popu, popu[indexT1].popu, years.z / 5.0f);
float rd1 = popuToRadius(popu1);
vec2 xy11 = vec2(xy0[i].floatx, xy0[i].floaty);
float dist = distance(xy00, xy11); //거리를 구한다.
float sumRadius = rd0 + rd1;
if ( sumRadius - dist > 150) //겹치면
{
vec2 v1 = normalize(xy11 - xy00);
float gap = sumRadius - dist;
float delta = gap * 0.35; //5%씩 움직인다.
xy00 = xy00 - v1 * mix(0.0, delta, rd1 / sumRadius);
intersectCount++;
} else {
}
} //for i
//되돌아간다.
if (intersectCount<3)
{
vec2 xy00ori;
if (center==0) {
xy00ori = vec2(xy0[index].orix, xy0[index].oriy) ;
} else if (center==1) {
xy00ori = vec2(xy0[index].altx, xy0[index].alty);
} else if (center==2) {
int sidocd = popu[index0].sggcd / 1000;
if (sidocd==11 || sidocd==23 || sidocd==31) xy00ori = vec2(958341,1963007);
else xy00ori = vec2(1033344,1766316);
}
if (xy00ori.x>1270000) xy00ori.x -= 90000; //울릉도 좌표 조정
if (judge) xy00ori.x += 550000; //특정값이 되면 기준점을 동쪽 멀리 보낸다.
if (xy00ori!=xy00)
{
float gap00 = distance(xy00, xy00ori); //거리를 구한다.
vec2 v00 = normalize(xy00 - xy00ori);
float delta00 = gap00 * 0.01; //1%씩 움직인다.
xy00 = xy00 - v00 * delta00;
//두 좌표 업데이트
atomicExchange(xy1[index].floatx, xy00.x);
atomicExchange(xy1[index].floaty, xy00.y);
//수정했으면 반영한다.
atomicCounterIncrement(atomicCnt);
}
} else {
atomicExchange(xy1[index].floatx, xy00.x);
atomicExchange(xy1[index].floaty, xy00.y);
//수정했으면 반영한다.
atomicCounterIncrement(atomicCnt);
}
}
}
|
cs |
알고리즘이라고 하기 민망하지만, 연산의 큰 골격은 다음과 같다.
1. 두 개 원의 인구에 따른 반지름을 계산한다. 예를 들어 A원의 반지름은 10이고 B원은 8이라고 하자
2. 두 원의 현재 거리를 계산한다. 계산된 거리가 12라고 하자.
3. 두 원의 거리가 18 이상이 되어야 두 원이 겹치지 않는다. 겹치는 부분을 한꺼번에 없앨 수 있을 정도로 두 원의 좌표를 재조정하면 움직임이 자연스럽지 못할 것이므로, 겹친 부분의 35%만 움직인다. 큰 원은 덜 움직이도록 한다.
이렇게 모든 원들 사이의 관계에 대해 루프를 돌면서, 각각의 경우만 신경써서 계산을 해주면 전체적으로 자신의 자리들을 잡아가게 된다. 당연히 한번에는 안되고 여러번 돌려주어야 한다.
1~3 부분을 한 프레임에서 10번씩 돌려주면 그럭저럭 빠르게 좌표들이 업데이트된다. 천천히 움직이려면 덜 돌려주면 된다. 물론 원의 수가 많아져서 계산량이 늘어나게 되면 brute force 방식으로 10번 돌리는 것은 효율적이지 못하므로, 그 때 가서 생각해본다.
그리고 각각의 원은 중력 중심점이 있다. 시군구 중심일 경우 각 시군구 중심은 각각의 원이 회귀하고자 하는 중심이 된다. 충돌이 적을 경우에는 이 중력중심점으로 이동하도록 한다.
시도 중심점일 경우 미리 셋팅해 둔 시도 좌표로 바꿔준다. 수도권/비수도권 중심일때는 위 코드에서처럼 직접 좌표를 지정한다.

위의 코드에서 읽어들이는 위의 구조체에서 orix, oriy가 시군구 중심점이다. altx, alty 는 시도 중심점이다. 이 두 쌍은 const 변수다. 수정하지 않는다.
floatx, floaty 에는 매 프레임마다 재계산 되는 좌표들을 업데이트한다.

기본적으로 이 좌표중심 데이터는 저렇게 두 벌을 읽어들인다. 이런 방식은 nBody 시뮬레이션처럼 셰이더 기반의 상호작용을 계산할 때 기본적인 부분인데, 두개의 버퍼들을 읽기/쓰기, 쓰기/읽기 로 swap 해가면서 작업하게 된다. 예를 들어 짝수 프레임에서는 0번을 읽어들여 계산 결과를 1번 버퍼에 쓰고, 그 다음 홀수 프레임에서는 1번 버퍼를 읽어들여 0번 버퍼에 계산 결과를 업데이트 한다. 그렇게 해야 충돌 이전의 좌표와 충돌 이후 업데이트한 좌표들을 섞지 않은 채 독립적(병렬적)으로 다룰 수 있기 때문이다.

인구가 증가하거나 감소하는 등, 특별한 문턱값을 넘어서는 순간 위의 버퍼에 시군구 순서대로 1을 기록한다. 시군구 배경을 그릴 때 이 버퍼를 읽어서 상호 연동하게 된다.

위의 그림처럼 원이 이동함과 동시에 해당 시군구 영역도 우측으로 이동한다. sggIndexBuffer는 원과 배경지도의 상호 정보 연계를 위해 사용한 버퍼다.
알고리즘이 단순하다보니 두 가지 단점이 있다.
1. 원들이 한데 뭉쳐있을 경우 서울에 속한 원이 경기도 바깥으로 튀어나갈 때도 있다. 즉 인접 공간 사이의 연결관계가 흐트러질때가 많다.
2. 다른 원들에 물리적으로 가로막혀서 가야할 클러스터로 아예 이동을 못하는 경우도 있다.
1번을 해결하려면 인접 연결 네트워크 데이터를 별도로 만들어준 후 계산해야 할 것 같다. 2번은 아예 그룹 속성 변수를 추가해서 다른 그룹에 속하게 될 경우 충돌을 무시하고 이동하도록 해야 할 것 같다.
하나의 원을 두 개 값의 비율로 분할해서 그리기

마스다 지수 표현의 경우 하나의 원을 분할해서 두 개의 데이터를 표시했다. 위 그림에서 아래 주황색은 65세 이상 인구, 위의 청록색은 20-39세 여성 인구다.
문제는, 사각형 막대가 아니라 원이다보니 양에 비례하도록 면적을 분할하는게 단순하지 않다는 것이었다.
찾아보니 원의 분할선을 구하는 함수가 있었다. (예전에 찾은 것인데 링크가 깨졌다)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
//원의 분할선 구하기. 분자에는 일부, 분모에는 총합
float divideCircleByRad(float numerator, float denominator) {
float k = numerator / denominator;
float rad1;
//by Newton Method, 원의 분할선 구하기
//http://mathforum.org/dr.math/faq/faq.circle.segment.html To refer initial value
float t0, t1;
if (k > 0 && k < 1) {
t1 = pow(12 * k * M_PI, 1.0f / 3.0f);
for (int i = 0; i < 10; i++) {
t0 = t1;
t1 = (sin(t0) - t0 * cos(t0) + 2.0f * k * M_PI) / (1.0f- cos(t0));
}
rad1 = M_PI - t1 / 2.0f;
} else if (numerator == 0.0f) {
rad1 = M_PI;
} else if (numerator == denominator) {
rad1 = 0;
}
return cos(rad1);
}
|
cs |
루프를 10회 반복하면서 근사값을 찾는 것 같다.
예를 들어 원의 면적을 1:4로 분할하고 싶으면 위의 함수에 각각 1과 (1+4)를 넣어서 결과값을 받는다. 값은 -1~1의 범위인데, 원에서 분할선을 그을 수평선의 높이가 된다. -1은 가장 밑, 1은 가장 위가 된다.
사실 원으로 그려보겠다고 작업을 시작해서 저렇게 함수까지 찾아가면서 분할선을 그은 것인데, 문제는 그려진 분할선을 보고 대략 몇 대 몇으로 분할되었는지 알아보기 어렵다는 결정적인 단점이 있다.
예를 들어 분할선을 동등한 10%씩 분할하면 아래와 같다.
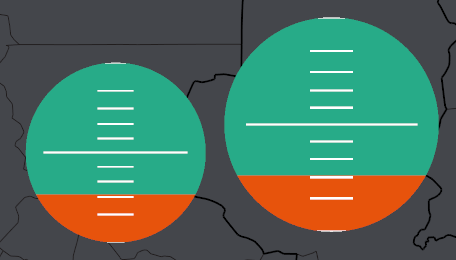
원은 그 기하학적 생김새 자체가 윗 부분과 밑 부분의 폭이 좁아질 수 밖에 없다. 그래서 10% 구간과 90% 구간은 두꺼울 수 밖에 없는데, 이러한 이유때문에 10% 분할선을 보고도 직관적으로 10%라고 알기 어렵게 된다.
아마도 이 쯤 읽으면 이런 의문이 생길것 같다.
"아니, 그래서 파이 차트식으로 분할하는 방식이 존재하는 것 아닌가??? "
맞는 말이다.
여기서는 원들이 많이 모였을 때 그림의 인상을 좀 단순하게 만들어보고 싶어서 이런 방식으로 시도해봤다.
원으로 시계열 변화량을 표현했더니.
원으로 무언가를 표시하는데에는 또 다른 단점이 있다.
변화를 표시해도 역시 직관적으로 알아보기 어렵다는 점.
아래 그림에서 검은색 테두리로 표현된 큰 원은 2000년의 고흥군 39세 이하 인구, 내부의 청록색은 2020년의 39세 이하 인구다. 그런데 얼마만큼 줄어들었는지 직관적으로 알아볼 수 있는가?

고흥군의 39세 이하 인구는 2000년에 33620명, 2020년에 12203명으로 36%로 줄어들었다. 바깥 원의 면적(검은색+청록색 면적 합계)이 100이라면 청록색 부분은 36이다. 이 차이가 직관적으로 와 닿는가?
직관적으로 와 닿는 사람들은 아마도 피자 라지 사이즈와 패밀리 사이즈를 가격 차이와 비교해가면서 합리적으로 주문할 수 있을 것 같다. 대부분의 사람들은 그렇게 하지 못한다.
증가와 감소 표현에 대한 색상 적용 문제 (복합 정보 표현)
인구 증감을 원으로 표현하는 초기 버젼은 아래와 같았다.

아래는 2020년 기준의 그림이다. 수도권 2개 유형, 비수도권 2개 유형의 네 가지 유형이 있다. 한 시점의 그림에서 시계열 변화량을 동시에 보여주고자 한 의도였다.

계란후라이처럼 표현된 그림은 수도권의 인구 증감 표현이다. 주황색 노른자는 1975년의 인구, 흰자처럼 보이는 바깥 테두리까지의 원의 크기가 2020년의 인구다. 즉, 흰색 부분은 45년동안 증가한 만큼을 가리킨다.
1975년 대비 인구가 줄어들었을 때는 다르게 그렸다. 바깥의 검은 테두리로 표현된 원의 크기가 1975년의 인구, 안쪽에 약간 어둡게 표현된 부분이 2020년의 인구다. 비수도권의 경우에는 푸른색 계열로 같은 규칙을 적용했다.
그런데, 몇 가지 문제가 있었다.
한 시점을 놓고 설명하면 정보가 인지되기는 하는데, 시계열 연속선상의 GIF를 만들고 나니 색상이 변하거나 흰색 부분이 생기는 순간, 같은 지역이 시각적으로 연속적이라고 인지되지 않았다. 마치 다른 개체처럼 인식되는 듯 했다.

그리고, 하나의 그림에 몇 가지 대비되는 정보들을 함께 표현하려고 하니, 집중도도 떨어지고 대비시켜야 하는 색상들의 가지수도 늘어났다. 그렇게해서 선택된 색상역시 전체적으로 조화롭게 보이지 못했다. 색상을 자연스럽게 안배하면 대비되는 정도가 떨어지는 단점이 있었다. 게다가 '환공포증'처럼 개구리알이나 눈알처럼 보이는 버블들의 이미지를 불편해하는 사람들도 있는 듯 했다.
그래서 아래처럼 바꿔보기도 했다.

일단 중심 부분 원의 색상만 동일하면 시계열상의 연속성은 잘 인지되는 것 같다.
마지막에는 한정된 정보 표현으로 집중도를 좀 더 높이고자, 아래처럼 증가 부분에 대한 부가적 정보 표현을 없애기로 했다.

그래서, 아래 처럼 마무리했다. 이 글의 처음에 등장한 그림이다.

이번에도 역시 몇 가지 시도 끝에 생각해볼거리를 남기고 여기서 마무리해본다.
'Function' 카테고리의 다른 글
| 맵 매칭(Map Matching) (2) | 2022.02.02 |
|---|---|
| 벡터필드 : 풍속 데이터로 바람 그리기 (0) | 2022.01.24 |
| 반응형 유동인구/매출액 Viewer (0) | 2021.12.20 |
| 지구를 그려보자 (0) | 2021.10.29 |
| 스마트서울 도시데이터센서(S-DoT)기온 데이터 시각화 (6) | 2021.10.11 |




