
데이터로 만든 이미지
3년 전에 프로세싱으로 한 해 동안의 인구 이동을 표현했었다. 580만개 가구 이동 각각을 선 하나로 나타냈는데, 적절한 결과물을 얻기 위해 선의 굵기와 색, 그리고 투명도를 바꿔가면서 수십장의 다른 이미지들을 만들었었다.

수치를 조금 작게 하면 너무 흐려지거나 조금 크게하면 모두 하얗게 날아가기도 했고, 선들이 모두 겹쳐진 최종 색상이 마음에 들지 않아 다시 작업하기도 했다.

그래서 결국 마지막에는 위와 같은 코드로 마무리했다. 랜덤하게 발생시킨 색상을 겹치고, 중간 진행 정도를 나타내는 t값을 세제곱 네제곱해보면서 적절한 변화 정도를 찾고, 굵기와 진하기는 영쩜 몇몇몇몇을 해야 적절한지를 여러차례 시도한 끝에 결정지었다. 그렇게 얻은 이미지를 마지막으로 포토샵에서 약간 조정했는데, 어두운 부분을 약간 밝게 해주는 정도만 리터칭을 했다.
그 결과물이 맨 위에 있는 그림이고, 그럭저럭 만족스런 결과물이었다.
그런데 사실 한 가지 아쉬운 점이 있었는데, 서울 언저리에 하얗게 날아간 부분이었다.
가깝고 먼 거리의 이동이 무수히 많이 겹쳐져서 색상의 한계 값인 255,255,255 에 도달했기 때문이었다. 이미지가 가진 정보는 단지 그것뿐이라서 아무리 어둡게 해봐도 주변과 디테일로 구분되지 않고 그냥 하얀 새똥이 뚝 하고 떨어진 것처럼 주변의 색상이 모두 같이 어둡게 변할 뿐이었다. 나는 분명히 선을 그렸지만 그 부분은 면이 되었다.
이 글에서 해보려는 이야기는 이제부터다. 고민은 바로 그 지점에서 출발했다.
이미지로서의 이미지
디테일은 없어서 아쉬웠지만, 물론 그 부분이 전달해주는 메시지가 없는 것은 아니다. '서울과 수도권에서 출발하거나 그 곳들로 도착하는 이동은 무수히 많다는 점'. 그리고 '서울 북쪽 보다는 주로 남쪽과 서쪽으로 이동이 발생했다는 점'과 같은 내용은 말할 수 있다.
그리고 물론 원천 데이터에는 수치가 있으므로 그 수치들을 조합하면 그저 '무수히 많다'가 아니라 몇명이 이동했다는 사실을 같이 언급할 수 있다. 그렇지만 여전히 데이터를 별도로 합산해야 하며, 이미지는 그저 느낌과 직관으로만 해석할 수 있을 뿐이었다. 곱셉과 보간과 보정이 여러차례 이루어져 만들어진 이미지에서, '무수히 많다' 정도 이상을 설명하기는 어려웠다.
프로세싱에서 OpenGL으로
프로세싱은 간편하기는 하지만 무언가 조금 더 해보려면 답답한 점들이 많았다. 우선 색상과 관련해서 그 안에서 무슨 일이 일어나는지 알 수 없었다. 물론 소스 코드를 뜯어보면 알 수 있었겠지만, 그렇게 알아내봤자 허용된 범위 이하로는 어차피 접근할 수 없다는 사실에는 변함이 없었다.
그러다가 작업의 바탕이 C++ / OpenGL로 넘어왔다. 여기서는 거의 모든 것을 다 직접 해주어야 하는데, 하다못해 이미지를 읽어오거나 쓰려고 해도 비트 수준에서부터 고민하지 않으면 원하는 바를 실행시킬 수가 없었다. 무척 번거롭기는 하지만 그 내용을 알게 되었을 때 한편으로는, '이것 이상은 어차피 안되는구나'라는 한계를 분명히 인지할 수 있으므로 아이러니하게도 마음이 편해진다는 부수적 효과도 있었다.
그럼 개인적 경험담은 그만 두고 색상 이야기부터 본격적으로 해보자.
색상
많은 사람들에게 익숙한 내용이겠지만, 보통의 경우에 색상 정보는 아래와 같이 저장되어 표현된다.
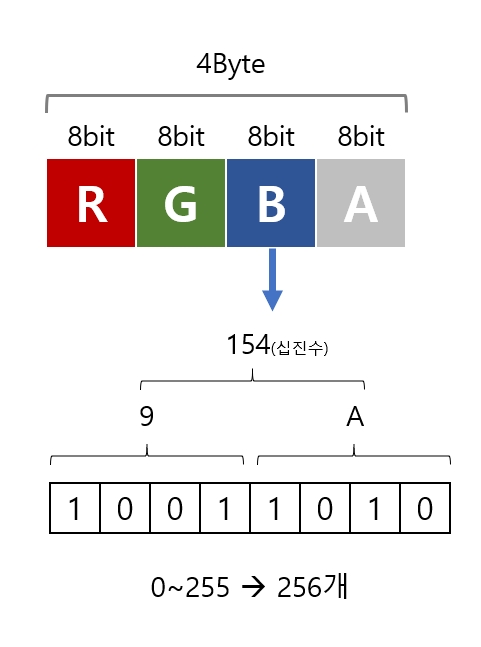
예를들어 포토샵에서 1920 x 1080 해상도의 빈 문서를 열면 기본적으로 포토샵은 가로 1920개 x 세로 1080개 = 총 2,073,600개의 픽셀을 준비한다. 그리고 각각의 픽셀은 4바이트의 공간을 필요로 한다. 그러므로 총 (2,073,600 x 4)/ 1024 / 1024 = 7.9MB 가 필요하고, 이미지를 압축 없이 저장하게 되면 약 7.9MB의 파일이 만들어지게 된다. (헤더나 레이어 등 부수적인 정보가 붙으므로 약 7.9MB라고 했다. 물론 psd 같은 경우 레이어로 관리되므로 용량은 더 증가할 수 있다)
이제 다시 픽셀 각각을 보자. 이 4바이트를 이루는 4개 각각의 바이트는 Red, Green, Blue, Alpha(투명도)의 정보를 담고 있는데 각각에게 할당된 저장공간은 1Byte, 즉 8bit다. 그러므로 8bit가 가진 한계인 0~255사이의 값들 안에서 각 색상의 강도를 표현할 수 있게 된다. 그래서 소위 말하는 '16만 컬러'는 RGB 값의 조합인 256 x 256 x 256의 값이기도 하다.
16만 컬러라는 것이 아주 많은 양 같지만, 또 그렇지도 않다. 예를 들어 RGB 포맷의 색상공간에서 검은색은 #000000이다. 여기에 아주 살짝 흰 색을 추가하면 #010101이 된다. 물론 아직은 '검은색'이라고 표현할 것 같다. 그런데 문제는 결국 그레이스케일로 진하기를 표현하려면 16만 단계가 아니라 256단계가 전부라는 사실이다.
OpenGL에서는 통상적으로 0.0~1.0 사이의 값으로 0~255에 대응하는 값을 표현하는데, 1/256 = 0.0039이므로 만약 R값에 0.003을 넣으면 마지막에 0x01(16진수 표현임)의 값으로 변환되어 저장된다. 소수점이라서 표현이 자유로울 것 같지만 어차피 색상 공간의 저장용량은 8비트 뿐이다. 따라서 R 값에 0.002를 넣으면 0x00과 0x01 사이의 무언가가 되는 것이 아니라 그냥 0x00 즉 검은색으로 남아있게 된다.
바로 여기서 문제가 생기는데, RGB 값을 (0.002, 0.002, 0.002)로 설정한 선을 백만개 겹쳐 그려도 결과는 아래처럼 그저 검은색으로 계속 남는다. 허용 범위 이하는 담아둘 곳이 없으므로 중간중간에 계속해서 버릴 수 밖에 없고, 결국 그려야 하는 선은 RGB = (0,0,0)이 되어버리므로 검은색 위에 계속 검은색만 그리게 되는 셈이다.

그런데 0.003으로 설정하면 아주 살짝 덜 검을 뿐이지만 분명히 (0,0,0)과는 차이가 있다.

그리고 이 선을 255개 누적시키면 아래처럼 흰 색 선이 된다.

그런데 이 선을 백만개 누적시켜도 선 하나의 밝기가 백만배가 되어 온세상을 비추는 일은 일어나지 않는다. 그저 255,255,255에 머무르게 된다. 왜냐하면 그게 바로 저장 공간의 한계이기 때문에.
아무리 연한 선도 255개가 겹쳐지는 순간 그저 하얗게 변해버린다.
그게 바로 맨 위의 인구 이동 그림에서 서울 주변이 하얗게 날아간 이유다. 주변 픽셀 모두 #FFFFFF ( =255,255,255)의 같은 RGB 값을 가지고 있으므로 아무리 밝기와 컨트라스트를 조정해보아도 바로 옆의 픽셀과는 구분할 수가 없다.
8bit 이상의 색상 공간
그런데 사실 8bit로 색상 하나를 표현하는 것은 고정된 기술의 한계가 아니다. 디스플레이 기기나 영상 인코딩에 관심 있는 사람들은 10bit 색상이라는 말을 들어봤을 것이다. 혹은 디지털 카메라에 관심 있는 사람들은 RAW 포맷이라고 들어봤을 것 같다. 이미지 포맷의 "계조가 풍부하다"는 말들을 하는데, 찍을 때는 그저 어둡게 보였던 밤하늘 RAW 이미지도 프로그램에서 조정하면 갑자기 별들이 나타나기도 하고, 역광이라 배경이 밝게 날아간 줄 알았는데, 밝기를 낮춰보니 그 안에 이런저런 디테일이 살아있을 때도 있다.
이건 결국 모니터의 표현 한계보다 파일이 더 많은 정보를 담고 있기 때문이며, 이것은 당연히 한 픽셀에 할당된 저장공간이 4바이트 이상이라 가능한 얘기다.
256 단계가 8bit 로 표현해서 2의 8승이라면, 10bit 색상은 2의 10승 즉, 1024단계를 표현할 수 있다. 그리고 놀랍게도 이미 RGBA 각각의 채널을 32bit(약 43억 단계)로 표현할 수도 있으며 표준 포맷으로도 유통되고 있다. 물론 파일의 용량은 딱 그만큼 커지지만.
OpenGL 에서도 표현 범위가 넓은 색 공간을 만들어서 작업할 수 있다. 이렇게 한 픽셀의 저장공간을 32 x 4 = 128bit 까지 확장시킨 이미지를 HDR (High Dynamic Range) 표현이 가능한 이미지라고도 하는데, 소프트웨어적으로 다루는 입장에서 아주 특별히 취급해야 할 부분은 없다. 물론 색상 공간과 포맷 하나하나를 변수 값으로 기술해주어야 하지만 전체적인 작업의 순서가 변하지는 않는다는 얘기다.
이를테면 OpenGL에서는 아래와 같이 워드프로세서의 '빈 문서'와 같은 바탕색공간을 마련하고 그림을 그리게 된다.
|
1
2
3
4
5
6
7
8
9
10
|
glCreateRenderbuffers(1, &fboOff.color0);
glNamedRenderbufferStorage(fboOff.color0, is128BitColor? GL_RGBA32F : GL_RGBA8,
scrW * safeBuffer, scrH * safeBuffer);
glNamedFramebufferRenderbuffer(fboOff.fbo, GL_COLOR_ATTACHMENT0,
GL_RENDERBUFFER, fboOff.color0);
glCreateRenderbuffers(1, &fboOff.depth32f);
glNamedRenderbufferStorage(fboOff.depth32f, GL_DEPTH_COMPONENT32F,
scrW * safeBuffer, scrH * safeBuffer);
glNamedFramebufferRenderbuffer(fboOff.fbo, GL_DEPTH_ATTACHMENT,
GL_RENDERBUFFER, fboOff.depth32f);
|
cs |
멀티샘플링을 적용시키지 않을 경우, 2번째 행에서 오프스크린 렌더 버퍼를 GL_RGBA8 값으로 써주는가, 혹은 GL_RGBA32F 값으로 써주는가의 차이 정도다.
물론 저장할 때도 크기가 차이나는 만큼 몇가지 변수값이 달라져야 하지만 아주 대단한 차이는 없다.
그리고 색상을 섞는 방법도 간단하다.
|
1
2
|
glBlendEquation(GL_FUNC_ADD);
glBlendFunc(GL_SRC_ALPHA, GL_ONE);
|
cs |
드로잉 명령을 내리기 전에 위와 같이 써주면,
(새로 쓸 색상RGB값) x (새로쓸 색상의 Alpha값) + (렌더버퍼(기존 색 저장공간)의 RGB값) x (ONE) = 새로운 색상의 색으로 계산된다. 컬러값들을 계속 누적시킬 수 있다.
색상의 표현범위가 넓은 HDR 방식은 수십만개 이상의 선을 겹쳐 그릴 때도 있는 데이터 시각화에 딱 응용하기가 좋다.
이제부터, 그저 하얗게 날아갔던 부분들과 희미한 선 한가닥 한가닥씩을 확대해보면서, 확장된 저장공간으로 과연 무엇을 할 수 있는지 살펴보도록 하겠다.
RGBA 128bit 색상공간의 이미지

위의 이미지는 단색으로 그린 2019년 1월 초 일주일 동안의 인구 이동 OD를 표현한 선들이다. 선의 RGB 값은 (1.0, 0.2, 0.1) 이고 마지막 Alpha 값을 0.01로 두었으므로, 선 하나가 그어질 때 [ 색상3채널 각각 x 알파값 ]의 결과인 (0.010, 0.002, 0.001)의 값이 검은색 바탕에 누적된다.
채널당 8비트 색상 공간에서는 채널당 0.0~1.0 사이의 값이 256단계로 분할되므로 0.003 이하는 쓸 수 없다고 했다. 그런데 채널당 32비트 색상 공간에서는 부동소수점 표현범위에 따라 소수점 이하로도 6자리까지 표현 가능하고, 1.0 이상의 값도 기록할 수 있다. 물론 0.0이 검은색, 1.0이 최대 밝은 흰 색이라는 점에는 변함이 없지만, 1.5의 값이 있다면 이미지의 노출값을 조정하여 추후에 디테일을 살려볼 수도 있다는거다.
이제 확대해서 픽셀의 색상을 몇 개 확인해보자.
안티에일리어싱 옵션은 적용시키지 않았으므로 선들 사이가 불연속적인것처럼 표현되었다. 대신 이미지를 압축 없이 저장할 경우 픽셀들은 처음에 선에 부여한 색상들을 그대로 담게 된다.

스포이드로 찍은 곳은 가장 흐린 붉은 색. 화면 팝업창 중간의 32-bit value 라고 표현된 곳이 바로 이 픽셀의 색상 정보를 보여주는 부분이다. 이 픽셀의 값은 (0.0101, 0.0020, 0.0010) 이다. 여기에는 선이 딱 1개 그려졌다. (부동소수점 방식이라 아주 깔끔하게 0.0100으로 떨어지지 않는 부분은 어쩔 수 없다.)

바로 근처의 픽셀 값은 (0.0201, 0.0040, 0.0020) . 앞의 두 배다. 여기에는 선이 딱 두개 겹쳐졌다. 출발지 행정동과 목적지 행정동 사이에 1월 첫 주동안 이사를 간 사람이 두 명이라는 얘기다.

이제 서초구 어딘가를 찍어봤다. RGB 값은 (1.3425, 0.2685, 0.1343).
아마도 여기저기 오가는 선들이 134개 누적되었을 것이다. 이동 선들이 상호 교차하고 있으므로 정확히 어디에서 어디로 가는 이동이라는 점까지는 알기 어렵지만, 중요한 것은 이미지의 픽셀 값에서 다시 선들이 겹쳐진 숫자를 계산할 수 있다는 점이다.
이미지에서 다시 숫자를 꺼냈다. OpenGL 라이브러리를 바탕으로 픽셀의 색상값이 누적되는 방식을 정밀하게 제어할 수 있을 때, 색상 값에서 다시 데이터를 뽑아낼 수 있게 된다.
데이터로서의 이미지

이미지를 다시 데이터로 사용한다는 개념은 사실 새로운 발견이나 응용은 아니다.
위성 측량같은 경우에도 DEM(수치표고모형) 이미지로 지구의 해발고도를 저장하는데, 위와 같이 그저 이미지로 보이는 DEM의 픽셀 하나하나에는 측량된 해발고도값이 들어 있다. 이미지의 역할은 단지 높은 곳을 하얗게 표현한 것일 뿐인데, 물론 그렇게 함으로써 평면적인 이미지에서 우리는 고저차를 대략 가늠할 수 있다. 그런데 거기에서 그치지 않고, 다시 저런 이미지를 바탕으로 지형을 모델링해서 여러가지 분석 작업에 사용하고 있다. 이미지라면 이미지고, 데이터라면 데이터인셈이다.
측량 분야는 아니지만 데이터 시각화 역시 '정확한 표현'은 그 '데이터' 시각화라는 개념과 통하며 매우 중요한 부분이기도 하다. 그런 맥락에서 이를테면 이런 질문들을 해본다.
- 데이터 시각화에서의 이미지 표현은 어떠해야 하는가?
- '적당히 아름다운' 그림을 넘어서서 무엇을 어떻게 표현해야 할 것인가?
- 우리는 많은 데이터 시각화 이미지들을 디지털 기기를 통해 보고 있으므로, 그저 눈으로 보는 것 이외에 파일이 담고 있는 정보의 무엇을 더 이용할 수 있을까?
데이터가 일련을 작업을 통해 래스터 이미지로 변환되긴 했으나, 사실 이미지도 데이터다. 파일을 열어보면 서로 다른 이진수들이 반복적으로 들어있기 때문이다. 그래서 '데이터로서의 이미지'라는 표현은 또 다른 동어 반복일 수 있지만 중요한 점은 그것이 동어 반복이냐 새로운 발상의 전환이냐처럼 개념적으로 선을 긋는의 문제는 아니다. 단지, 습관적으로 하고 있는 작업들에서 하나의 돌을 더 얹어 무엇을 조금 더 해볼 수 있을 것인가를 고민하자는 얘기다.
HDR 조정
그럼 드디어 처음의 고민, 그러니까 하얗게 날아간 부분을 해결해보자.

만약 위의 이미지가 jpg라면 하얀 부분은 더 이상 복원할 수 없다. 그렇지만 128bit 이미지에서는 가능할 수도 있다.
우선 스포이드로 찍어보니 RGB 값이 (20.0, 7.3, 3.6). 이미 통상적인 한계인 1.0을 훌쩍 넘어섰다. 포토샵에서는 20.0 이상은 모두 20.0으로 표현되는 것 같다. 실제로는 R값이 36.8 정도 될 것이다. 포토샵에서는 표현되지 않으나, 이미지는 물론 이 정보를 담고 있다는 얘기다.

여기서 노출을 -5로 조정해본다. 노출 -5는 각각의 RGB 값을 2의 5승 = 32로 나누어주는 보정이다.
밝기가 줄어들었고 하얗게 날아갔던 부분들이 조금씩 구분되기 시작한다. 그런데 서울 안쪽은 아직 뭉개진 것처럼 보인다.

더 줄여본다. 2의 10승 즉, RGB 값을 1024로 나누어줬다. 흐리긴 하지만 이제 비슷해 보이던 부분들이 서로서로 구분되고 있다. 아마도 휴대폰에서 이 글을 읽고 있다면 그림이 거의 검게 보일 것 같다.
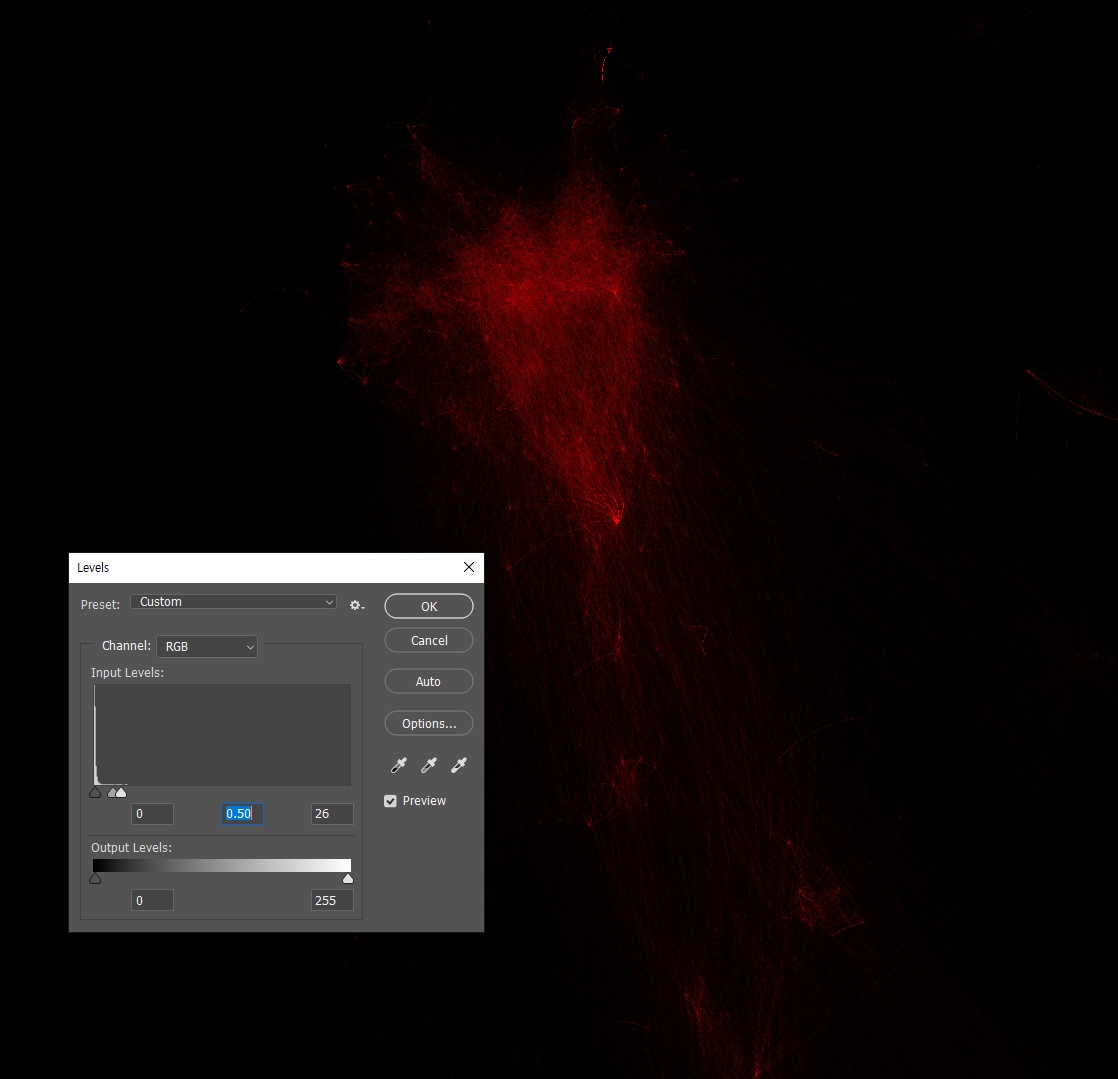
인위적으로 레벨 분포를 조정해보았다. 이제 디테일이 드러난다.
이미지는 데이터의 디테일을 온전히 담고 있었다.
너무 붉은 색만 있어서 눈이 불편하다면 이번에는 다른 그림으로 보자

역시 이선저선 섞여 있고 수도권이나 대구 부산 중심부는 하얗게 날아갔지만,

노출 값을 낮추면 날아갔던 부분의 디테일이 살아난다. 사진에서 역광으로 피사체를 찍었을 때 하얗게 날아간 배경이 RAW 이미지에서 다시 살아나는 원리와 같다.
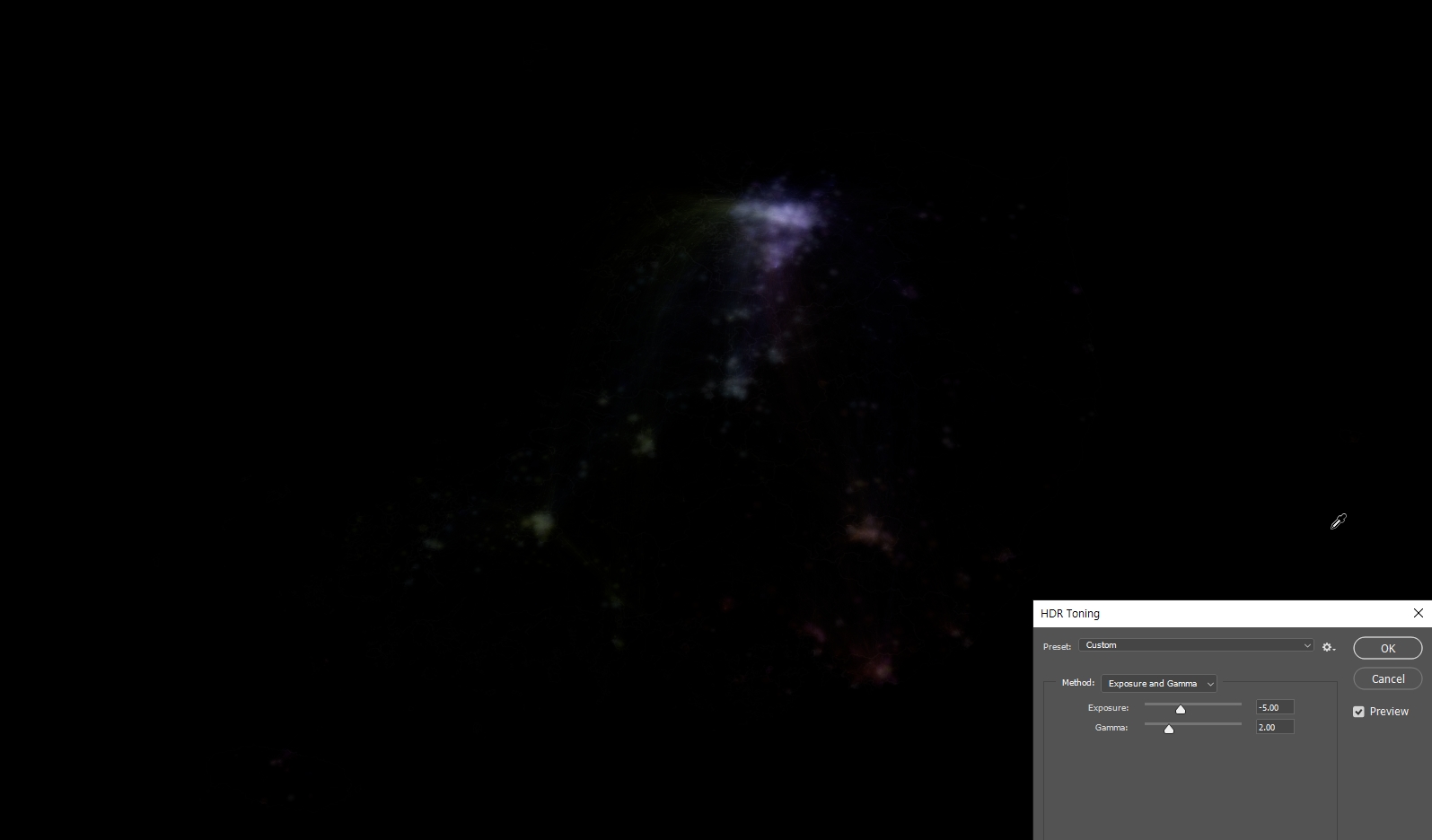
적절히 다른 값을 조절하면 일부 지역만 필터링되어 남는다.
이동의 개수, 즉 선의 개수만큼 색상 값이 정확히 곱해져 들어가 있다면 특정한 값을 경계로 필터링하는 것도 가능해진다. 즉, 한 장의 이미지로 일정 값 이하의 이동만 보거나, 일정 값 이상의 이동만 선택적으로 보는 것이 가능해진다는 얘기다. 물론 인구 이동의 경우 선들의 경로가 중간중간에 겹쳐지는 상황이라 정확한 이동만큼 필터링하기는 어렵지만 격자맵 같은 경우에는 충분히 가능하다.
그런데 문제가 생겼다.

아까 예시로 든 빨간색 선만 있는 이미지다.
분명히 선이 134개 겹쳐져 있다고 설명할 수는 있지만, 보기에 그렇게 편하지는 않다.
많은 데이터 시각화에서 여러가지 색상을 써서 서로 다른 정보를 표현하는데, 만약 단색 이미지에서만 숫자를 셀 수 있다면 그저 DEM 이미지 이상도 이하도 아닌셈이다.
무슨 말이냐고? 그럼 이제 이 글의 마지막 챕터를 시작해보자.
세 가지 색상의 선들이 겹쳐진 이미지를 다시 세 가지 색상의 선들로 분해하기

위의 그림은 일 주일 동안의 인구이동(전입신고)데이터를 시각화한 결과다. 보통의 경우 여러가지 다른 이동들을 표현할 때 이와 같이 몇 가지의 다른 색들을 사용해서 표현하기 마련이다.
128bit 색상공간을 가진 이미지에서 단색으로 표현하였을 때 누적된 값들을 찾을 수 있다는 사실은 위에서 확인했는데, 그렇다면 여러 색상을 섞어서 사용한 경우는 어떨까?
그림을 확대해보자.

위의 그림의 왼쪽 중간에 스포이드가 있다. 이 그림에서 붉은색 계열 중 가장 흐린 선인데, (0.0031, 0.0003, 0.0003)의 RGB값을 가지고 있다. 즉 붉은 계열의 선 1개가 있을 때의 색상 값이다.

이제 오른쪽 가운데쯤에 스포이드가 보이는가? 이 픽셀의 값은 (0.4350, 0.2625, 0.3369)다. 이 지도는 세 가지 색상의 선들로 이루어졌는데 아마도 그 세 가지 색상이 서로 섞여 있는 것 같다.
이제 이 픽셀에 각각의 색상 몇개가 섞여 있는지 알아내보겠다.
음........?
무슨 약을 파냐고....?
고등학교때 종종 먹던 약이다.
우선 당연히 어떤 색상의 색을 섞었는지는 알고 있어야 한다.
A선의 색상은 (0.0030, 0.0003, 0.0003). 붉은색 계열의 아주 희미한 선
B선의 색상은 (0.0003, 0.00045, 0.00288). 푸른색 계열 아주 희미한 선
C선의 색상은 (0.0003, 0.00304, 0.00208). 녹색 계열 아주 희미한 선
저 픽셀의 값은 (0.4350, 0.2625, 0.3369)다.
저 픽셀에 A선이 a번, B선이 b번, C선이 c번 지나가고 있다.
그러므로 0.0030이 a번, 0.0003이 b번, 0.0003이 c번 겹쳐져서 0.4350의 수치가 결정되었다.
수식으로 쓰면 아래와 같다.
(0.0030 x a) + (0.0003 x b) + (0.0003 x c) = 0.4350
그리고 다른 값들을 이용하여 이런 식을 두 개 더 만들 수 있다.
자. 여기까지 왔으면 눈치챈 사람이 있을 것 같다.
고등학교때 배운 삼원일차연립방정식.
우리는 RGB 세 개의 슬롯을 가지고 있으므로 색상 3개까지는 방정식을 만들어 분해할 수 있을 것 같다.
물론 알파채널까지 이용하면 4개의 색상도 알아낼 수 있을 것 같은데 이미지를 만들어 낼 때 몇 가지 불편한 점이 있기 때문에 우선 3개가 결합된 이미지만 분해해보기로 한다.
삼원 일차 연립 방정식은 역행렬을 이용하면 풀 수 있다. 물론 이 해법은 고등학교때 배우지 않았지만.
어쨌거나 저 방정식을 푸는건 그리 어려운 일이 아니다.
이제 다시 행렬을 만들어보자.
하필 색상 값들이 비슷해서 좀 헷갈릴 수도 있겠지만, A선의 색상이 (3 X 3) 행렬에서 1열에 해당한다. 1행이 아니라 1열이다.
(0.0030, 0.0003, 0.0003) (a) (0.4350)
(0.0003, 0.00045, 0.00304) (b) = (0.2625)
(0.0003, 0.00288, 0.00208) (c) (0.3369)
조금 귀찮아서 그냥 텍스트로 썼는데, (3 x 3) 행렬과 (3 x 1) 행렬을 곱한 후 (3 x 1) 행렬과 비교하는 행렬식이다.
(3 x 3)행렬을 A라 할 때, A의 역행렬을 각 변의 좌측에 곱해주면 좌항은 a,b,c만 남아서 곧바로 해를 구할 수 있다.
풀이과정은 검색해도 금방 나오고, 그리 대단한게 아니므로 답만 구해보겠다.
물론 지금처럼 픽셀 하나는 그냥 손으로 풀어도 금새 계산할 수 있다.
두둥. 결과는 바로,
a는 132.8833
b는 56.259
c는 64.907
부동소수점 방식이라 깔끔하게 안 떨어졌을 것 같은데, 아마도 a는 133번, b는 56번, c는 65번 겹쳐졌을 것이다.
3개 색상의 색상 값중 어느 서로간에 완전한 배수 관계만 아니라면 어느 픽셀이든 해를 계산할 수 있다.
사실 수학적으로 빈틈이 없음에도 불구하고 이게 정말 되는 것일까 의문이 들었다.
부동소수점 때문에 대략 근사값으로 해가 나와서 사실은 잘 분해가 되지 않는게 아닐까? 하는 의구심.
의구심을 떨쳐버리려면 직접 한 장의 이미지를 분해해보는 수 밖에.
다시 전체 이미지를 보자.

서울인천경기에서 출발하는 선들은 붉은색 계열.
부산대구울산경북경남에서 출발하는 선들은 푸른색 계열
나머지 모두에서 출발하는 선들은 녹색 계열
위에서 예로 든 이미지이고 각각이 A선, B선, C선에 해당한다.
역행렬을 먼저 구했더니 아래와 같이 나왔다.
(337.726, -10.3661, -33.5601)
(-12.4393, -265.63, 390.023)
(-31.4869, 369.291, -54.4218)
이제 각 픽셀마다 rgb값과 이 역행렬을 곱해주면 각 픽셀마다 겹쳐진 3개 선들의 개수가 나온다.
그걸 3장의 이미지에 저장해주면 끝.
OpenGL을 사용한다면 컴퓨트 쉐이더를 이용해서 GPU로 순식간에 계산할 수 있다.
그래서 얻은 이미지는, 다음과 같다.

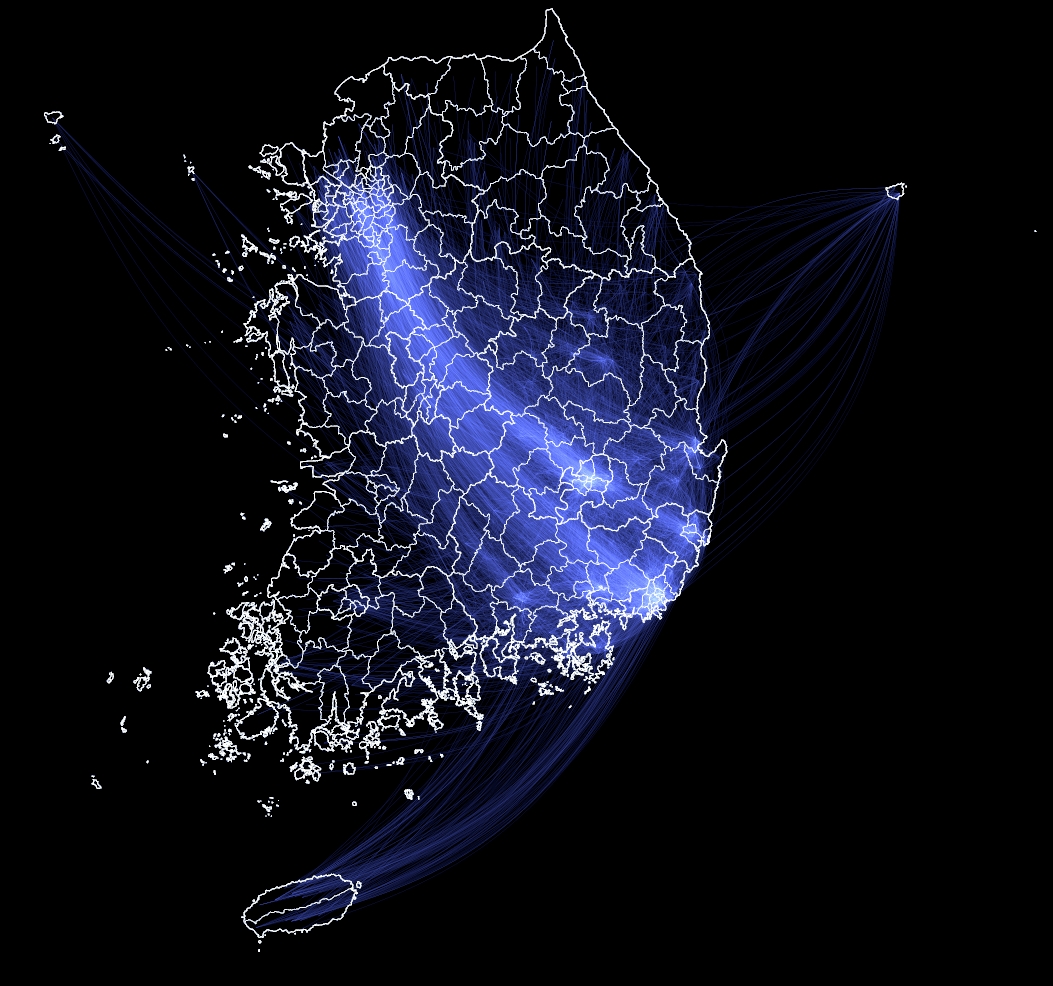

아주 깔끔하게 분리되었다.
정말 될 줄 몰랐는데, 그래서 색상과 시점을 바꿔서 한번 더 해봤다. 사실 위에처럼 색상 설정을 할 것이라면 차라리 그냥 R채널로만 한장, G채널로만 또 한장, B채널로만 마지막 한장을 그리면 아주 간단하게 분해할 수 있다. 그래도 데이터 시각화는 보기도 좋아야 한다. 그래서 색상 역시 선택에 따라 다양하게 사용할 수 있으므로 다른 색상에서도 정말 잘 되는지 확인해야 했다.
각각 선의 색상은 다음과 같다.
(1.0, 0.1, 0.1) 붉은색계열
(0.1, 0.35, 0.9) 푸른색 계열
(0.95, 0.75, 0.3) 노란색 계열
그리고 위에는 일주일치 이동이었는데, 이번에는 1년의 모든 이동을 넣어봤다. 선 하나하나가 한명씩이므로 1000만개 가까이 된다.
그리고 위에는 안티에일리어싱을 적용하지 않았고, 아래이미지는 적용해본 것.

이것이 1년 이동을 누적하여 얻은 이미지
이제 똑같은 방식으로 분해해보자.



안티 에일리어싱도 원래 색상의 벡터 값에서 RGB간의 비율을 잘 유지하면서 계산되는 것 같다. 분해가 잘 되었다.

물론 디테일도 살아 있다.
아, 참. 각 선들의 개수를 세기로 했었지.

오른쪽 상단 스포이드 지점은 (0.0381, 0.0038, 0.0038)
처음에 색상값인 (1.0, 0.1, 0.1)을 1/1000로 흐리게 해서 겹쳤으므로 저 지점에는 38개의 선이 겹쳐져 있을 것이다.

많이 진해 보이는 곳은 (2.5579, 0.2559, 0.2559) 저 곳에는 선이 2558번 겹쳐 있을 것이다.
숫자라는게 이렇게나 정확하고 무섭다.
이로서 [수백만개 선들의 적층과 재분해]는 성공적으로 끝.
'Function' 카테고리의 다른 글
| 통계청 집계구 인구를 격자로 재할당하기 (7) | 2020.12.15 |
|---|---|
| Nvidia Mesh Shader 코드를 작성해보자 (2) | 2020.05.17 |
| 국토교통부 실거래가 데이터 전처리 (10) | 2020.04.19 |
| 공시지가 - 전국 모든 땅의 가격은 얼마나 높고 낮은가? (0) | 2020.03.02 |
| 텍스트 빈도와 네트워크 인터랙티브 시각화 (6) | 2019.08.31 |




